Introduction to Electricity

Why learn about electricity?

Electricity and magnetism are foundational components of our everyday life from the phone or computer you are reading this on to the power grids that light up your house. Furthermore, understanding the nuances of interactions between particles and objects using these physical applications can give us a much deeper understanding of our biology, which can allow us to further develop models and explanations that can provide useful insights for how our body and brain function. We will go over more of these nuances in the following sections, but first it is important to have a solid background on the physics behind electricity.

Electric Potential

You are likely already familiar with the concept of charge interactions, such as rubbing a balloon on your hair, causing it to rise. Similarly, by rubbing certain objects with different types of cloths can build positive or negative charge that creates forces. These interactions can be quantified by magnitudes of force through Coulomb's Law, F = (kq₁q₂)/r², where F is the force on both particles, k is a constant, q₁ and q₂ are the charges of the two particles respectively, and r is the distance between them. This website is primarily conceptual based, so we will not be going in depth for the mathematical applications, but take a moment to observe the equations and think about how F changes as you alter other values. You'll notice that:

As charge increases, the force increases
As the distance increases, the force decreases

Alternatively, we can introduce the concept of an electric field (E), which can be found through the equation E = F/q = (kq)/r² where q is the charge of the source particle. This means that a stationary particle with charge q₁=1 will always have the same electric field at a given location. In other words, the electric field doesn’t act on another particle, but rather alters the region of space regardless of whether there’s another particle or not. However, you can probably intuitively tell that the large charge will cause a large repulsion. So why is E unchanged between the two? This is because the force between two particles can be found by multiplying the electric field by the charge that is being influenced. Therefore, q₂=10000 would have a large repulsion (force) but an unchanged electric field. In other words, The electric field can be thought of as a measure of the force a first particle will exert on a unit charge that can be replaced by any other charge being influenced.

We have now explained electric charge and electric field, which describe the forces that influence a charged particle. However, how can we determine the possible, or potential, movement of a particle? We do this with potential energy, which refers to energy that is stored in the system which has the potential of being converted. This could be into motion, but not necessarily. Potential energy tells us the energy stored in the configuration, but does not by itself predict future states.

If we wanted to determine the amount of distance that a particle could move with a certain amount of potential energy, we would need to determine the amount of work, W, given a certain amount of force, F to move a distance Δx, which can be modeled through W = F * Δx. Notice that the greater the force required or the greater the distance traveled, the greater the required work is to complete the task.

Another important quantity is electric potential V, which is what we get by dividing the potential energy by charge. This is an important quantity because we can directly measure differences in it, so that the difference in potential between two locations separated by Δx, the potential difference is ΔV = E*Δx. Notice the similarities between this equation and the equation for work above.

Circuits

We have seen in the previous section how we can model immediate charge interactions between individual particles. However, one electron likely will not be able to power your entire house, but rather billions upon trillions (on the scale of 6.28*10^18 electrons per second in just 1 amp!). We use circuit diagrams to demonstrate systems that control the flow of these electrons. As we will observe later, using these circuits to model real life systems can also include external input, which can act as a limitation to using these diagrams in biological systems.

There are a few common components to a circuit diagram:

Batteries, which raise the potential of electrons and therefore, provide energy for the circuit
Resistors, which resist the motion of electrons by lowering their potential energy
Capacitors, which can be charged by storing opposite charges on either side of its plates
Switches, which can open a circuit or close a circuit

Using these components and their associated values, we can calculate the current (I), or the charge flowing in the wire per second, and the resistance (R), or the measure of how much the flow of charge is resisted when a voltage (V) is produced across the resistor. The relationship between these values can be summarized through Ohm's law, V = I*R.

These circuits are governed by what are known as Kirchoff's Laws. They are as follows:

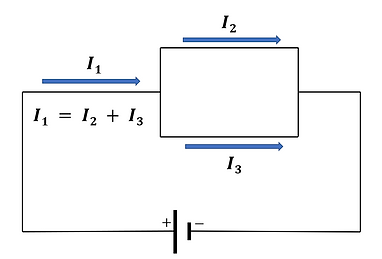
1) Kirchoff's junction law is an application of the law of conservation of charge, which tells us that the total current leaving a junction must equal the total current that entered it.

2) Kirchoff's loop law is an application of the law of conservation of energy, which tells us that the total electric potential around any closed loop must be zero.

RC Circuits

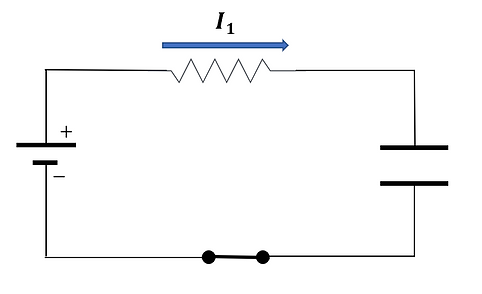
Resistance and capacitance can interact with each other within what is known as a resistance-capacitance, or RC circuit. Just like in a normal circuit, capacitors can store charge without allowing it to move across while resistance resists the flow of current. This setup can be visualized in the diagram to the left.

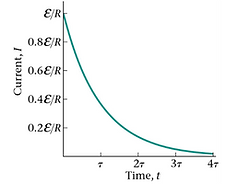
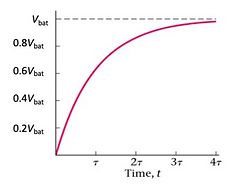
Assuming that the capacitor has not been charged, charge will build up on the capacitor as soon as the switch is closed. As we learned before, like charges repel, so the movement of charge towards the capacitor will become increasingly more difficult over time. Therefore, as the capacitor is charged (graph on the right), the current decreases (graph on the left) as a result of charge repulsions.

This building of charge on the capacitor can later be released, or discharged, to create a small temporary current. When not equilibrating to the voltage of a battery, the opposite charges on the capacitor want to move away from their like charged plate and therefore quickly move to the opposite end of the capacitor. This quick movement of electrons can be used to create energy through current.

As we will see later on, this same RC circuit can be used as an imperfect model of electrical signals throughout the cells in your body, which you will read about in the following section.

Continue ->